쉬운 예시로 알아보는 베이즈 정리 (Bayes Theorem / Bayes Rule) - Posterior, Likelihood, Prior
Machine learning분야를 공부하다 보면 주로 초반에 Bayes theorem 혹은 Bayes rule에 대해 공부하게 됩니다. 처음에 다루는 내용이라 쉽다고 생각할 수도 있겠지만, machine learning분야를 계속해서 공부하다 보면, 정말 중요한 개념이고, 어려운 개념이라는 것을 알 수 있습니다. 그래서 그런지 저도 자주 해당 개념을 반복해서 보게 되는 것 같습니다. Bayes theorem을 설명하는데 가장 자주 드는 예시가 “연어”(salmon)와 “농어”(sea bass)를 구분하는 문제입니다. 물론 이를 machine learning에 대한 전반적인 예시로 들기도 합니다. 이번 포스팅에서는 상투적이지만, 널리알려진 “연어”와 “농어”의 예시를 이용해 Bayes theorem에 대해 설명하고자 합니다.
1. 연어와 농어를 구분하자
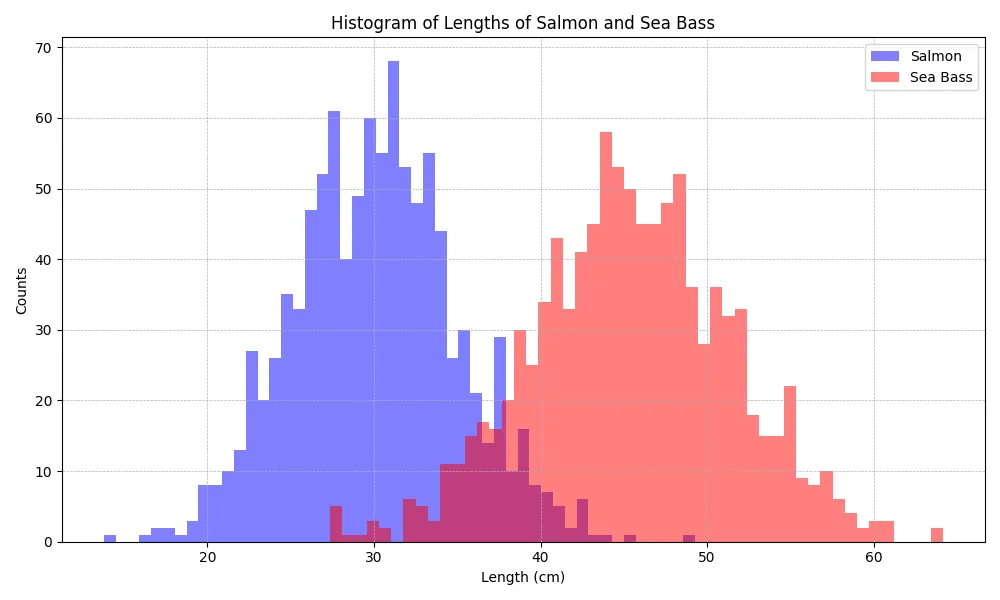
바닷속에 존재하는 물고기는 오직 연어와 농어만 있는 세상에서 산다고 생각해 봅시다. 이런 세상에서 물고기를 잡으면, 무조건 연어 또는 농어가 잡히게 되는데, 이를 구분하는 기계를 만든다고 생각해 봅시다. 좋은 방법은 아닌 것 같지만, 일단 길이로 판단해 볼까요? 그래서 부산 앞바다에서 물고기를 잡으면 길이를 측정하고, 연어인지 농어인지 사람이 직접 판단해 봤습니다.
그림 1. 측정된 연어와 농어의 길이 분포
그래서 열심히 물고기를 잡아 길이를 측정하고, 연어인지 농어인지 판단해서 histogram을 위와 같이 구했습니다. 그럼 이제, 물고기를 잡고 길이를 측정한 다음에 대충 35~38cm를 기준으로, 길이가 더 길면, 농어(sea bass), 짧으면 연어(salmon)로 판단하면, 얼추 길이에 따라서 물고기를 구분할 수 있어 보입니다. (물론 약간의 에러를 가지고 있긴 하겠습니다.) 왜 이런 판단을 했을까요? 그건 데이터의 분포에 따라, 길이가 더 길면, 농어의 빈도수가 더 높고, 짧으면 연어의 빈도수가 더 높다는 것을 확인할 수 있었고, 이는 나름 합리적으로 보입니다. 그러면 이 과정을 확률적인 표현방법을 통해 표현해 보겠습니다. 일단, histogram을 확률분포로 나타내 보겠습니다.
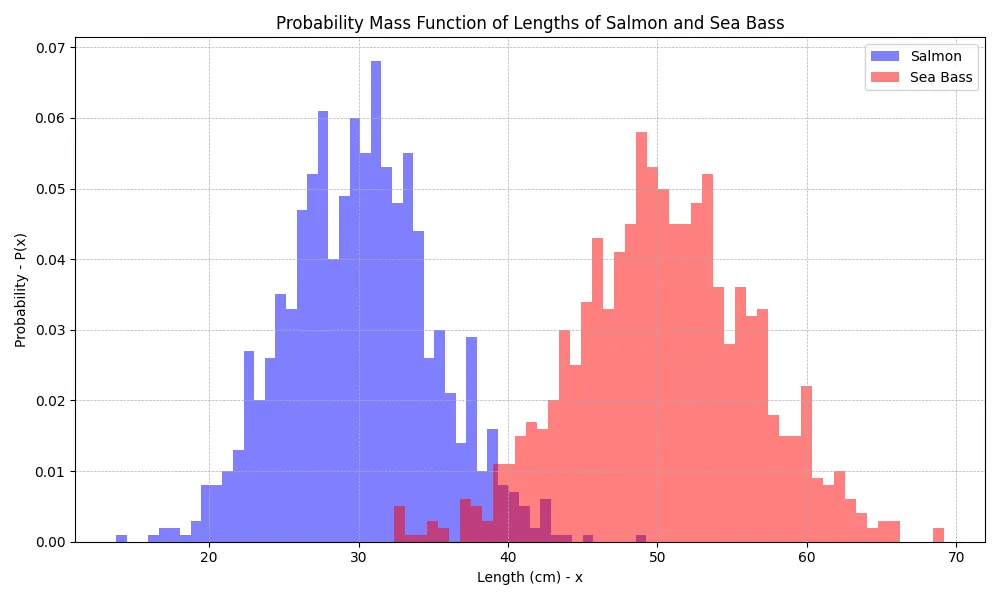그림 2. 연어와 농어의 길이에 대한 Probability Mass Function
단순히, 위의 histogram에서 전체 개수를 나눠주면, probability mass function으로 표현할 수 있습니다. (혹시나 해서 언급드리자면, probability mass function은 probability density function의 discrete 버전입니다.) 여기서 생선의 길이를 “x”라고 표시하겠습니다. (이를 전문용어로 random variable이라고 합니다.) 그러면, 길이 “x”가 결정되면, 연어와 농어일 확률을 다음과 같이 표현할 수 있습니다.
\[P(w|x)\]좀 더 구체적인 예로, 만약 길이 “x”가 30 이라면… 연어와 농어의 확률 값은…
\[P(w=연어|x=30)=0.06\] \[P(w=농어|x=30)=0\]이런 상황에서 자연스럽게, 생선의 길이 “x”가 30라면, 연어일 확률이 더 높으므로, 생선은 연어라고 판단할 수 있겠습니다. 하지만…. 이 접근 방법은 잘못 되었습니다. 위의 사고 과정은 많은 사람들이 잘못 생각하는 접근 방법이라서 언급해 봤습니다. 사실 위의 그래프는
\[P(x|w)\]| 으로 표시해야 하며, w가 결정되면 $P(x)$가 결정되게 되는 형태입니다. 애초에 연어와 농어만 존재하는 세상에서 $P(w=연어 | x=30) + P(w=농어 | x=30) = 0.06$ 은 잘못되었다는 것을 알 수 있습니다. (합은 당연히 1이 되어야 합니다.) |
그래도 직관적으로 생각해 봐도, 주어진 생선의 길이 x에 대해 어떠한 생선이 높은 확률로 나올지 결정해야 하는 것은 변함이 없습니다. 즉,
\[P(w|x)\]이 문제를 풀어야 한다는 것입니다. 이를 확률 용어로 Posterior(사후 확률)이라고 부릅니다.
한편 위에서 언급한
\[P(x|w)\]는 likelihood(가능도)라고 부릅니다. 아마 여기까지 읽으신 분들은 이런 생각을 하실 수 있습니다. 아까 위에서 물고기의 길이에 따라 판단하는 법은 제법 합리적으로 보였는데, 굳이 posterior를 계산해야 할 필요가 있을까요? 그냥 likelihood를 보고 판단해도 무리는 없어 보이는데요? 하지만, 이런 질문을 던져볼 수 있습니다. 만약 부산 앞바다가 아니라, 대서양에서 물고기를 잡게 되면, 부산 앞바다에서 획득한 likelihood를 그대로 사용할 수 있을까요? 연어와 농어의 길이에 대한 특징이 비슷하다면, 그대로 사용해도 괜찮을 것이라 생각하실 수도 있습니다. 하지만, 만약, 대서양에서는 농어가 잘 안 잡히는 지역이라면, 위의 접근 방법을 그대로 이용할 수 있을까요? 여기서부터 베이즈 정리는 시작됩니다.
2. Posterior - 사후 확률
앞에서 언급하였지만, 정리를 한번 하고 진행할까 합니다. 먼저 posterior입니다. Posterior는 어떠한 데이터의 특징 (위의 예시로는 물고기의 길이)이 주어졌을 때 w의 확률분포를 의미합니다. 만약, 물고기 길이 x가 40cm 라면, 연어일 확률 0.3, 농어일 확률 0.7 이 나와서 농어로 판단하게 되는 것입니다. 이를 수식으로 표현하면,
\[P(w=연어|x=40)=0.3\] \[P(w=농어|x=40)=0.7\]로 표현이 됩니다.
여기서, $w_{1} = 연어$, $w_{2} = 농어$ 라고 하고, 정리해 보자면,
\[P(w=w_{1}|x) > P(w=w_{2}|x)이면, 연어\] \[P(w=w_{1}|x) < P(w=w_{2}|x) 이면, 농어\]로 표시하게 됩니다. 즉, 특징 x가 주어졌을 때 높은 확률을 보이는 class로 선택하겠다는 것입니다. 결국 이 posterior를 구하는 것이 대부분의 machine learning에서 추구하는 것이지만, 매우 어려운 문제라고 할 수 있습니다.
3. Likelihood - 가능도
Likelihood의 정의는 다음과 같습니다.
\[P(x|w)\]이는 특정 클래스가 정의되고 난 후, x에 대한 확률을 나타냅니다. 위의 길이에 대한 histogram과 probability mass function이 사실, likelihood를 나타내는 그래프들입니다. Likelihood는 실제 문제를 푸는 과정에서 반드시 구하게 됩니다. 왜냐하면, 이는 데이터의 관측을 통해 얻어낼 수 있는 정보이고, 어떤 데이터의 분류문제 등을 풀 때, 큰 힌트가 되기 때문입니다. 연어와 농어 예시에서 실제 물고기를 잡고, 길이를 측정하고, 연어인지 농어인지 사람이 판단하는 모든 과정이 사실은 likelihood를 알아내는 과정입니다.
하지만, 앞서 언급하였듯이, likelihood를 알게 되었다 해도, class를 판단하는 measure로 사용하기는 어렵습니다. 그 이유는, 각 class에 대한 확률을 모르기 때문입니다. 만약, 어떤 지역에서는 연어가 전혀 안 잡히고, 농어만 잡히는 지역이라면, 단순 길이를 보고 판단하는 것이 의미가 있을까요? 그러기 때문에 prior이라는 개념이 도입됩니다.
4. Prior - 사전 확률
각 class에 대한 확률을 prior(사전 확률)로 정의합니다.
\[P(w)\]이를 연어와 농어의 예로 표현해 보면, 자연계에 연어가 존재할 확률과 농어가 존재할 확률을 의미합니다. 그런데 현실적으로, 전 세계에 연어와 농어가 존재할 확률을 정확하게 알 수 있을까요? 아마 평생 동안 연어와 농어의 개수를 세어도 실시간으로 죽고 태어나기 때문에, 파악하는 것은 거의 불가능할 것입니다. Likelihood를 관측을 통해 어느정도 파악했다 해도, prior를 정확하게 알수가 없으니, posterior를 계산하는 것이 매우 어렵다는 말이 나오는 것 입니다. 그러한 이유로, 해당 부분은 보통 직접적으로 계산하지는 않고, 가정이나, domain에 따른 사전지식을 통해 설정해 둡니다. 가령 생물학자들이 파악한 정보에 따르면 연어와 농어의 개체수는 대략적으로 3:7이 비율로 구성되어 있다는 사전 지식을 얻었다고 한다면,
\[P(w=연어)=0.3\] \[P(w=농어)=0.7\]로 정의할 수 있고, 이를 likelihood와 함께 반영한다면, posterior를 계산할 수 있는 희망이 생기게 됩니다.
5. Bayes Rule
앞서 알려드린 개념들을 요약 정리하면 다음과 같습니다.
Posterior : P(w|x), 주어진 특징 x에 대해 클래스 w일 확률. 우리가 구하고자 하는 것. Likelihood : P(x|w), 각 클래스 w에 대해 특징 x의 분포. 데이터에 대해 우리가 관측할 수 있는 정보. Prior : P(w), 각 클래스 w의 확률. 사전 지식으로 정의된 클래스 w의 분포. 자, 여러 번 강조하였듯이, posterior가 우리가 구하고자 하는 목표인데, 이는 likelihood와 prior, 그리고 고등학교 때 배운 조건부 확률을 이용하여 계산할 수 있습니다. 먼저, 고등학교때 배운 조건부 확률은
\[P(A, B)=P(B|A) P(A)=P(A|B) P(B)\]으로 정의됩니다. 그리고 이를 적절하게 변형하면,
\[P(A|B)=\frac {P(B|A) P(A)}{P(B)}=\frac {P(B|A) P(A)}{ \sum_{A} P(B|A) P(A)}\]으로 표현할 수 있는데, 이 형태에서 위에서 정의한 것들을 대입하면…
\[P(w|x)=\frac {P(x|w) P(w)}{P(x)}=\frac {P(x|w) P(w)}{ \sum_{w} P(x|w) P(w)}\]로, 표현할 수 있습니다. 결국, 위의 식을 통해 posterior를 계산할 수 있고, 이는 likelihood와 prior의 곱으로 표현할 수 있다는 것을 의미합니다. 추가적으로 위의 P(x)에 대한 용어도 있는데 이를 evidence라고 합니다. 연어와 농어의 예시에 evidence를 대입하면, 임의의 물고기를 잡았는데, x cm일 확률을 말해 줍니다. 특정 sample하나에 대해 x가 정해지기 때문에, 사실 evidence는 상수라 할 수 있습니다. 이렇게 보면, evidence는 단순 상수 이기 때문에, 중요한 파라미터로 보이지는 않지만, variational inference라는 기법에서 매우 중요한 정보로 쓰이게 됩니다. 자, 이제 마지막으로 정리해 보면,
\[Posterior=\frac {Likelihood \times Prior}{Evidence}\]이 되겠습니다. 위 식을 Baye’s Equation, Baye’s Rule이라고 부릅니다.
그림3. Posterior 분포
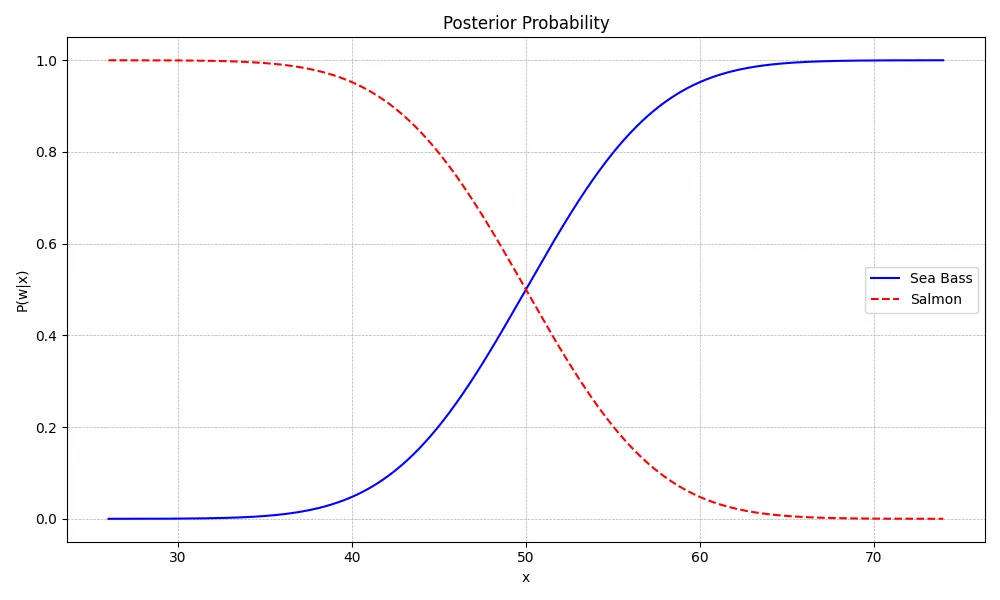
위 그림은 prior에 적절한 값을 부여하여 그려본 posterior 입니다. 위 그래프는 대략적인 분포로 그려본 posterior 입니다. 농어와 연어 어느쪽에 가중치를 더 주느냐(prior)에 따라 분포는 달라질 수 있습니다. 위의 그래프를 읽는 법은 x(물고기의 길이)가 일단 정해지면, y축 값을 모두 읽어서 어느 클래스가 더 높은 확률을 가지는지 확인합니다.